Window to Viewport Mapping (or) Window-to-Viewport Transformation

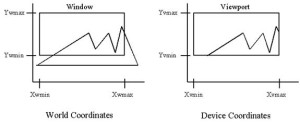
Window to Viewport Mapping:

In Window to Viewport Mapping, we need to map coordinates from “Window values to the “Viewport” values. So when mapping is done between the coordinates from window to viewport are called Window to Viewport Mapping. In window to viewport mapping, we map rectangular region of 2D device position or scene to the device. We must notice that, both window and viewport are represented by rectangular regions. So both these rectangles are aligned with the coordinate axes.

You can understand Window to Viewport mapping easily, when you go through the following figure.

Both Window and Viewport are shown in above figure,                                               

From above figure,

Coordinate Units of Window = (xw, yw)

Coordinate Units of Viewport = (xv, yv)

Where,

xw = X-coordinate in window

yw = Y-coordinate in window

xv = X-coordinate in viewport

yv = Y-coordinate in viewport

Now, let us map (xw,yw) to the (xv,yv).So when mapping takes place then the relative places (positions) in Two areas (window and Viewport) are the same.

In the above figure also showed that,

xw_min = Minimum X-coordinate value in window

xw_max = Maximum X-coordinate value in window

yw_min = Minimum Y-coordinate value in window

yw_max = Maximum Y-coordinate value in window

xv_min  = Minimum X-coordinate value in viewport

xv_max = Maximum Y-coordinate value in viewport

yv_min = Minimum X-coordinate value in viewport

yv_max = Maximum Y-coordinate value in viewport

So to keep the same relative displacement both in the viewport and as in the window. To maintain same relative position, we need

(xv- xv_min)/( xv_max– xv_min) = (xw- xw_min)/( xw_max– xw_min)  —   Eq 1

(yv- yv_min)/( yv_max– yv_min) = (yw- yw_min)/( yw_max– yw_min)  —   Eq 2

From the above equations, we need to find out the values for Viewport coordinate points (xv,yv).Remember above Eq 1 and Eq 2,since without which we cannot get Viewport mapping coordinate units.

Mapping xw to xv:

From Eq 1,

(xv- xv_min) = [( xv_max– xv_min)/( xw_max– xw_min)] * (xw- xw_min)

Where, Scaling factor ∆x = [( xv_max– xv_min)/( xw_max– xw_min)]

Therefore, xv = {∆x * (xw- xw_min)} + xv_min

Mapping yw to yv:

From Eq 2,

(yv- yv_min) = [( yv_max– yv_min)/( yw_max– yw_min)] * (yw- yw_min)

Where, Scaling factor ∆y = [( yv_max– yv_min)/( yw_max– yw_min)]

Therefore, yv = {∆y * (yw- yw_min) } +  yv_min

When scaling factors same ∆x = ∆y, then we can say that relative proportions of Objects are maintained. As far as Character strings are concerned, they can be handled in two ways. And generally a simple window to viewport mapping concerning Character strings, keep up a constant character size irrespective of the viewport area (may be increased or decreased) and this is used generally when character font cannot be changed. If characters formed with line wise segments then this window to viewport mapping can be conveyed as a sequence of line transformations. This mapping is referred as Window to viewport mapping.