Computer Graphics Reflection Transformation is explained in detail.Computer Graphics is the Sub part of the Main Computer Science subject.Computer Graphics Reflection is used to reproduce the objects of Main images again which are shown on shiny surfaces or else using in mirrors. In Computer Graphics subject, we need to study transformations such as Reflection and Shear. So Reflection is as explained below. The term’s meaning is available in the name itself “Reflection” that is a “Mirror Image” or “Duplicate Object” or “Replica” of an original object. Reflection is also a transformation in Computer Graphics.
Basically the mirror image of any image for 2D reflection is generated with respect to the “Axis of Reflection”. For that we need to rotate main object 180 Degrees about the reflection axis.
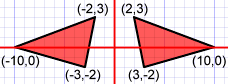
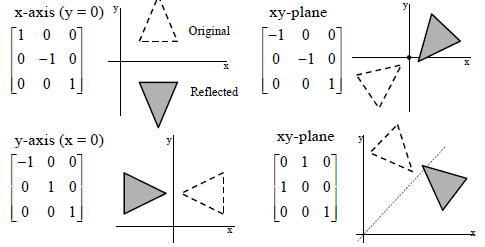
Following figures are shown for better understanding of Computer Graphics Reflection.In the above figure, it shows the half of the above image is reflected with respected to the X-axis. So there we may choose axis of reflection in the XY plane. One must remember that, when the reflection axis is a line in the XY plane, say X-axis, the rotation path about this X-axis is in a plane which is perpendicular to the XY plane. So Image gets reflected with respect to any axis say X-axis or Y-axis. Generally the image is original plane is represented with the points say 1,2,3, where as the reflected image is denoted with the same numbers with dashes say 1’,2’,3’ and likewise.
As this image is reflecting with respect to the X-axis, the reflection transformation obviously keeps X-values same. But one must notice that, the image “Flips” 180 degrees and the values of Y of coordinate positions. And similarly when the image gets reflected with respect to Y-axis is shown figure. As mentioned in the above X-axis, case the point gets reflected with respect to Y-axis and obviously point gets flipped.
Types of Computer Graphics Reflection:
Transformation in Computer Graphics Reflection is broadly classified in to Two Categories. They are,
I. Horizontal Reflection
II.Vertical Reflection
I. Horizontal Reflection:
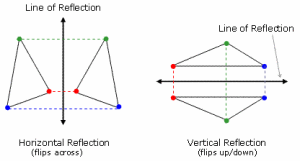
When Image gets flipped across, then the Image reflection is known as Horizontal Reflection. And here image gets reflected with respect to the Y-axis.
II.Vertical Reflection:
When Image gets flipped up and down, the reflection is referred as Vertical Reflection. For easy understanding, we are providing detailed image analysis, which show both Horizontal and Vertical Reflections.
Generally Reflection about any line in Computer Graphics is represented by any line,
y = mx + b
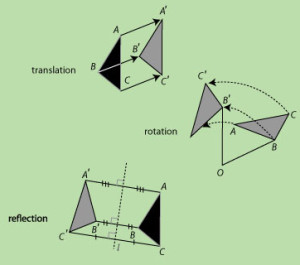
The line y = mx + b, can be achieved with a combination of translate-rotate-reflect transformation. In this several transformations Translation, Rotation and Reflection took place. For Instance, consider a line, so what do we do first? Yes first we translate the image, so that it generally moves towards one of its side from origin point. So then we rotate the same object to one of the coordinate axes and reflect it about that axis. Now we restore the object to its actual position with the inverse rotation and translation.
The above image illustrated by transformations Translation, Rotation and Reflection. We request you to understand keenly those transformations shown in above figure.Computer Graphics Reflection transformation is generally implemented with respect to the coordinate axes or its coordinate origin as the scaling transformation with t minus (negative) scaling factors.
Notice that, the reflection matrix we regularly see is of 1’s and -1’s.So the matrix is also set to +1 or -1.Remember,in Computer Graphics Reflection the values whose magnitudes are greater than 1,they shift the mirror image farther (longer) from the reflection axis. In contrast, the values less than 1 generally bring the mirror image closer to the reflection axis. So the image distance basically depends on the reflection matrix.